Summary of Projective Geometry

In this article will emphasize on some important characteristics and invariants with respect to transformations in projective geometry.

Some properties in projective geometry

The following properties are important to know if you want to work on stereo image processing, photogrammetry computer vision which contains 3D reconstruction, depth estimation and so on. For different dimensions in projective space we would have some important properties which are somehow similar:

In 1D projective space:

The cross-ratio while linear transformation in constant (See the following figure):

$CR = \frac{AC . BD}{BC . AD}$

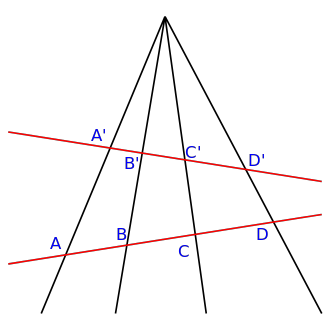
Fig. 1: Cross-ratio [1]

In 2D projective space:

Point at infinity, as we know projective space has more points than Euclidean space and they are called ideal points or points at infinity in which the last element of homogeneous coordinate is zero (Two parallel lines will cross each other at infinity):

$\tilde{P}_{ideal} = \left(\begin{array}{c} x \0& y \0& 0 \end{array}\right)$

Line at infinity. In a perspective projection, ideal points will be located on a line which is called horizon. The line which connects two ideal points can be calculated by the cross product of them:

$L_{ideal} = P_{ideal,1} \times P_{ideal,2}$

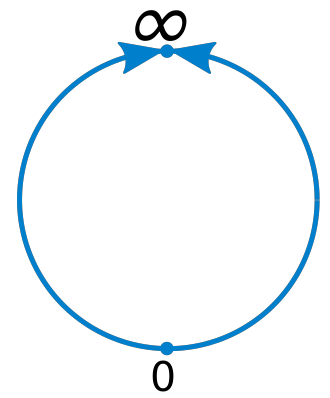
Two parallel lines cross each other at two points (at each end of lines), so the real projective line can be considered as a circle, See the following figure. The ideal line will be defined as:

$L_{ideal} = \left(\begin{array}{c} 0 \0& 0 \0& c \end{array}\right)$

Color Spectrum — Fig. 2: Real Projective Line [2]

Duality of line and point. In one hand, the cross product between two points will result a line which connects the points, on the other hand, the cross product between two lines will result in a point which is where the lines intersect, so by changing the elements the result will be changed from line to point and vice versa:

$L = \tilde{P}_1 \times \tilde{P}_2$

$P = L_1 \times L_2$

Colinearity. Three points are located on a same line if:

$det[\tilde{P}_1, \tilde{P}_2, \tilde{P}_3] = 0$

Three lines intersect in a point if:

$det[L_1, L_2, L_3] = 0$

Incidence of point and line:

$\tilde{P}^TL = 0$

Incidence of line and point:

$L^T\tilde{P} = 0$

In 3D projective space:

There is a duality between point ( 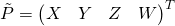$\tilde{P} = {\begin{pmatrix} X & Y & Z & W \end{pmatrix}}^T$ ) and plane ( $\pi = {\begin{pmatrix} a & b & c & d \end{pmatrix}}^T$ ).
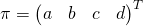Like 2D, ideal point ( 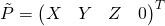$\tilde{P} = {\begin{pmatrix} X & Y & Z & 0 \end{pmatrix}}^T$ ) is where 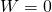$W = 0$ . And ideal plane ( 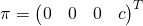$\pi = {\begin{pmatrix} 0 & 0 & 0 & c \end{pmatrix}}^T$ ) is where $X = Y = Z = 0$ .
Three points define a plane if:

$\left(\begin{array}{c} \tilde{P}_1^T \0& \tilde{P}_2^T \0& \tilde{P}_3^T \end{array}\right) \pi = 0$

Three planes intersect in a point if:

$\left(\begin{array}{c} \pi_1^T \0& \pi_2^T \0& \pi_3^T \end{array}\right) \tilde{P} = 0$

Coplanarity. Four points are in a plane if:

$det[\tilde{P}_1, \tilde{P}_2, \tilde{P}_3, \tilde{P}_4] = 0$

Intersection of four plane in a point:

$det[\pi_1, \pi_2, \pi_3, \pi_4] = 0$

Incidence of point and plane:

$\tilde{P}^T\pi = 0$

Incidence of plane and point:

$\pi^T\tilde{P} = 0$

Summary

2D Properties

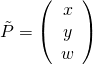
Point	$\tilde{P} = \left(\begin{array}{c} x \0& y \0& w \end{array}\right)$	Line	$L_ = \left(\begin{array}{c} a \0& b \0& c \end{array}\right)$
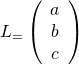
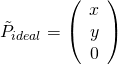
Ideal point	$\tilde{P}_{ideal} = \left(\begin{array}{c} x \0& y \0& 0 \end{array}\right)$	Ideal Line	$L_{ideal} = \left(\begin{array}{c} 0 \0& 0 \0& c \end{array}\right)$
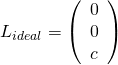
Connect 2 points	$L = \tilde{P}_1 \times \tilde{P}_2$	Intersect 2 lines	$P = L_1 \times L_2$
Colinearity	$det[\tilde{P}_1, \tilde{P}_2, \tilde{P}_3] = 0$	intersect 3 lines	$det[L_1, L_2, L_3] = 0$
incidence point on line	$\tilde{P}^TL = 0$	Line through a point	$L^T\tilde{P} = 0$

3D Properties

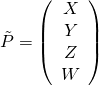
Point	$\tilde{P} = \left(\begin{array}{c} X \0& Y \0& Z \0& W \end{array}\right)$	Plane	$\pi = \left(\begin{array}{c} a \\ b \0& c \0& d \end{array}\right)$
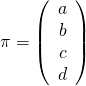
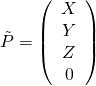
Ideal point	$\tilde{P} = \left(\begin{array}{c} X \0& Y \0& Z \\ 0 \end{array}\right)$	Ideal Plane	$\pi = \left(\begin{array}{c} 0 \0& 0 \0& 0 \0& c \end{array}\right)$
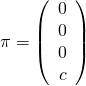
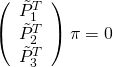
3 points define a plane	$\left(\begin{array}{c} \tilde{P}_1^T \0& \tilde{P}_2^T \0& \tilde{P}_3^T \end{array}\right) \pi = 0$	Intersection of 3 plane	$\left(\begin{array}{c} \pi_1^T \0& \pi_2^T \0& \pi_3^T \end{array}\right) \tilde{P} = 0$
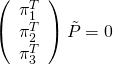
Coplanarity	$det[\tilde{P}_1, \tilde{P}_2, \tilde{P}_3, \tilde{P}_4] = 0$	Intersection of 4 planes	$det[\pi_1, \pi_2, \pi_3, \pi_4] = 0$
Incidence of point & plane	$\tilde{P}^T\pi = 0$	plane through a point	$\pi^T\tilde{P} = 0$